Antes de falar sobre a decomposição de vetores, vamos relembrar a respeito de seno, cosseno e tangente em um triângulo retângulo (triângulo onde há um ângulo de 90º).
No triângulo retângulo acima temos os catetos B e C (pois são os lados do triângulo que entre eles, formam o ângulo de 90°) e a hipotenusa A (lado que está oposto ao ângulo de 90°, que não “toca” neste ângulo).
Seno de alfa = cateto oposto / hipotenusa
Seno de alfa = B / A
Cosseno de alfa = cateto adjancente / hipotenusa
Cosseno de alfa = C / A
Tangente de alfa = cateto oposto / cateto adjacente
Tangente de alfa = B / C
Aplica-se o mesmo raciocínio para o ângulo téta, tendo que prestar atenção qual é o cateto adjacente e oposto em relação á ele. O cateto oposto de um ângulo não é o mesmo para outro ângulo!
Sabendo isso, vamos ver como é um vetor.
Todo vetor tem tamanho, direção e sentido.
Tamanho: o quanto ele mede
Direção: está na horizontal? vertical? forma 45°?
Sentido: a “seta” é pra cima? pra baixo? direita? esquerda???
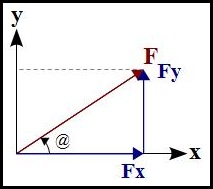
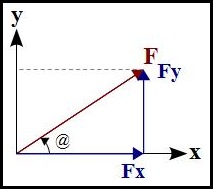
Aí está o vetor F no plano cartesiano que forma um ângulo @ em relação ao eixo X (chamei o ângulo de @ ao invés de alfa, beta ou gama pra facilitar na hora de mostrar as contas).
Chegou a hora de decompor suas forças em seus respectivos eixos (em X e Y).
Mas e agora? Como achar as forças Fx e Fy? onde uso seno, cosseno e tangente?
Resposta: Simples! Basta mudarmos a força Fy de lugar para ter uma melhor visualização.
Pronto, formamos um triângulo retângulo onde a força F é a hipotenusa e as forças Fx e Fy são os catetos.
Sendo assim vamos analisar esse triângulo retângulo da mesma forma que o outro no começo deste post.
| sen(@) | cos(@) |
| sen(@) = Fy / F | cos(@) = Fx / F |
Pronto! Simples né? (claro, fica simples depois que aprende hehe)
Caso o exercício dê as forças Fx e Fy e peça pra você achar o valor da força F, faça o mesma esquema, bastando apenas isolar a força F na fórmula.
Atenção!
Observe que o ângulo utilizado aqui é o que está entre a força F e o eixo X.
Se o exercício passar o ângulo que está entre F e o eixo Y e você ficar perdido, não conseguir usar o seno ou cosseno, calcule o ângulo entre F e o eixo X, pois entre os dois eixos, X e Y, o ângulo é de 90º. Daí é só fazer: 90 menos o outro ângulo (entre F e o eixo Y), obtendo assim o que está entre F e o eixo X (no nosso caso, o ângulo @).
E pra terminar, vamos achar quanto vale o ângulo @.
tg(@) = Fy / Fx
@ = arctg (Fy/Fx)
Esse arctg é aquele botão na calcularora que está escrito tan-¹.
Na tg, você tem o ângulo e acha o valor da tangente deste ângulo. Arctg é o contrário. Você passa o “resultado” e ela informa o ângulo. Para seno e cosseno é a mesma coisa (sen-¹ e cos-¹ na calculadora)
Obs.: Preste atenção se a calculadora está fazendo os cálculos de seno e cosseno em graus ou radianos. Sen(90) em graus é diferente de sen(90) em radianos.
Espero que a explicação tenha sido clara e objetiva.
Outra hora faço uma explicação mais detalhada, pois todo o desenvolvimento foi feito apenas com um vetor no 1º quadrante. Podemos somar vários vetores e cada um estar em um quadrante diferente, mas isso é assunto pra um outro dia.