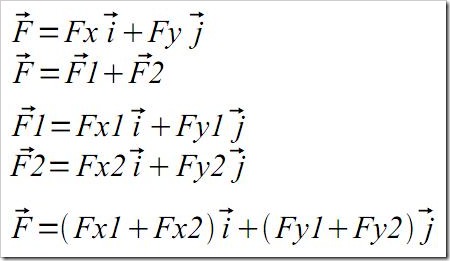Finalmente sentei pra fazer essa segunda parte a respeito de decomposição de vetores. Agora vai!
Vamos ver o contrário agora, onde se tem os valores do vetor nos eixos X e Y e assim determinar seu módulo e inclinação.
Tendo os valores do vetor no eixo X (Fx) e no eixo Y (Fy) temos a seguinte fórmula para achar a força F:
Fiz questão de deixar as forças entre parêntes para evitar erros na hora de fazer a conta. Caso Fx seja um valor negativo (Fx=-a):
-> (-a)² é diferente de –a².
O valor de F sempre será positivo na hora de se calcular, independente dos valores de Fx ou Fy, conforme mostra na figura acima.
Como foi dito acima, o que muda são os sentidos (pra cima, pra baixo, esquerda, direita…) das projeções do vetor F (Fx em Fy) sobre os eixos.
Os vetores podem possuir o mesmo módulo (tamanho), mas o q diferencia um do outro são a direção e sentido (como mostrado na 2ª figura).
Para achar o ângulo já há uma explicação na 1ª parte sobre decomposição de vetores, mas, resumindo:
tg(@) = Fy / Fx
@ = arctg (Fy/Fx)
Esse arctg é aquele botão na calcularora que está escrito tan-¹.
Onde:
Na hora em que for achar o valor do ângulo, considere Fx e Fy sempre positivos (em módulo). Depois de encontrado o ângulo, verifique os sinais de ambos os vetores para ver em qual dos 4 casos acima o ângulo é posicionado.
Soma/Subtração dos vetores
Não tem segredo. Quando for somar dois vetores (F1 e F2 por exemplo), terá que decompor ambos (nos eixos X e Y). Daí é só somar as forças de seus respectivos eixos que você terá o vetor resultante.
Uma observação rápida
Outra forma de se expressar um vetor é informando os valores de suas projeções nos eixos.
Onde o i informa o valor no eixo X e j no eixo Y. Para achar o valor de F (seu módulo), basta usar a outra fórmula dada no começo desta aula.
Então, para somar/subtrair dois vetores fica assim:
Obs.: Considere os sinais!!!
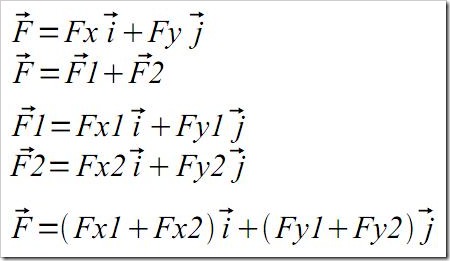
F é a força resultante da soma dos vetores F1 e F2!
Caso precise somar 3 ou mais vetores e você se perca como calcular, faça as contas para dois, e com a resultante some com e 3º vetor, e assim por diante.
Fica a 2ª e a última (provável) parte a respeito de decomposição de vetores. Foi bem básico, nada aprofundado, mas espero que tenham entendido bem pra quando se aprofundarem mais no assunto.
